Вопросы подготовки моделей к расчёту

В данной публикации будут описаны некоторые моменты, связанные с подготовкой модели к различным типам расчёта. Практически во всех случаях, первым этапом является построение модели и оптимизации её элементов для упрощения расчёта. На примере моделей макета и рамы тепловоза, вам будет показано несколько вариантов оптимизации.

Рис. 1 Твердотельная модель рамы тепловоза.

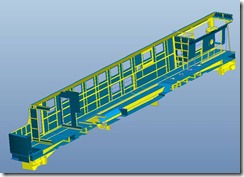
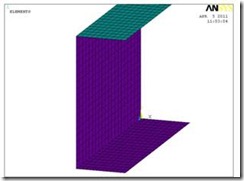
В зависимости от типа расчёта следует выбрать тип построения конструкции: твердотельная или поверхностная (в случае поверхностного построения следует указывать толщину сечения для каждой поверхности). Для упрощения распознавания различных частей модели, рекомендуем вам заранее покрасить вашу модель в различные цвета. В нашем примере мы выбрали поверхностное построение модели, что значительно уменьшает количество уравнений и экономит время (смотрите рисунки 1-3).

Рис. 2 Тонкостенная модель рамы тепловоза.

Рис. 3 Тонкостенная модель макета тепловоза.

Наложение цветов, которые заметны на рисунках 2 и 3, происходят из-за интерференции поверхностей. Такое может быть либо при поверхностном построении модели (рисунок 2), либо при пересечении элементов в твердотельной конструкции.

Одним из методов упрощения геометрии для решения в CAE системах является избавление от мелких второстепенных элементов (отверстия, рёбра), сдвиг положения элементов и прочее, но при этом нужно учитывать важность того или иного элемента в конкретной части модели.

Рис. 4 Упрощенная геометрия.	Рис. 5 Изначальная геометрия.
Рис. 6 Упрощенная геометрия	Рис. 7 Изначальная геометрия.

Данные выводы были сделаны по сравнениям результатов расчёта изначальных и упрощенных элементов модели.

Результаты частотного расчета модели (рисунок 4)	Результаты частотного расчета модели (рисунок 5)
SET	TIME/FREQ	SET	TIME/FREQ
1	1024.5	1	1037.4
2	1024.5	2	1037.4
3	1024.7	3	1042.8
4	1024.7	4	1042.8
5	1028.9	5	1039
6	1028.9	6	1039
7	1029.8	7	1044.6
8	1029.8	8	1044.6
9	1036.4	9	1044.8
10	1036.4	10	1045.1

Результаты частотного расчета модели (рисунок 6)	Результаты частотного расчета модели (рисунок 7)
SET	TIME/FREQ	SET	TIME/FREQ
1	88.533	1	84.816
2	88.686	2	84.891
3	89.071	3	85.994
4	89.716	4	86.350
5	90.634	5	87.933
6	91.841	6	89.341
7	93.355	7	90.102
8	95.196	8	92.574
9	97.388	9	95.326
10	99.952	10	97.138

В современных CAE системах расчёт машиностроительных конструкций проходит чаще всего с помощью метода конечных элементов (далее МКЭ). Это приближённый метод, суть которого заключается в разбиении всей конструкции на простые элементы (треугольники, квадраты, кубы, пирамиды, призмы) и расчёт будет производиться не всей конструкции, а системы простых элементов, что в следствии облегчает работу и затраты времени (см. рис 12-13). Результаты вычислений будут менее точные по сравнению с аналитическим способом расчета, который использовался ранее. Для проведения расчётов в программных пакетах требуется создать, конечно-элементную модель.

Рис. 12 Объёмная КЭМ	Рис. 13 Поверхностная КЭМ

Рис. 14 Поверхностная КЭМ с достаточным для данных задач размером элемента

При твердотельной конструкции количество уравнений значительно выше, чем в поверхностной (8505 в твердотельной и 5166 в поверхностной), при этом если геометрия не очень сложная (не имеет большое количество отверстий, имеет большие промежутки и пр), то можно так же увеличивать размеры элемента, что уменьшит количество уравнений (уменьшилось до 93 уравнений). В случае если имеем протяженные элементы, то их желательно привести к балочной или оболочечной. Сначала следует задать ряд параметров для создания конечно-элементной сетки. Для начала следует определить тип элемента. Это зависит от того, какой тип построения конструкции вы выбрали. Для поверхностных конструкций применяются элементы группы Shell, а для твердотельных – Solid. В каждой и групп имеется несколько типов элементов, которые отличаются количеством узлов (в зависимости от необходимой точности вычислений), форма элемента (зависит от геометрии вашей конструкции).

Далее следует задать тип материала. В CAE системах тип материала задаётся физическими свойствами: модуль упругости, коэффициент Пуассона, плотность материала и другие в зависимости от типа расчёта.

При построении конструкции поверхностным способом следует задать толщину сечения на каждом участке.

Для верности вычисления конструкции должна происходить сходимость узлов элементов пересекающихся или сопрягающихся поверхностей. Для этого желательно разделить исследуемую поверхность на некоторое количество частей. Это можно осуществить различными операциями. Далее (в следующих публикациях) будет показано несколько примеров выполненных в ANSYS Mechanical APDL 13.0.

Затем следует разбиение на элементы полученных поверхностей. Это можно осуществить при помощи задания количества или размера элементов на линии (поверхности).

После этого следует задание закреплений и нагрузок в зависимости от типа анализа.

При выполнении всех пунктов ваша модель готова к расчёту.

С уважением Теплиций Леонид, Халченко Сергей, Дунаев Александр !